Громадянська Освіта
http://osvita.khpg.org/index.php?id=1271919405
Популярні математичні статті в The New York Times
автор: Стівен Строґатц [Steven Strogatz]
джерело:
Зміни, у які ми можемо повірити
The New York Times, 11.04.10 Західна аналітична група, 13.04.10
Задовго до того, як дізнався, що таке числення, я відчував, що є щось особливе стосовно нього. Мій батько говорив про нього шанобливим тоном. Як дитина Депресії він не зміг відвідувати коледж, але десь протягом свого життя – можливо, впродовж часу, проведеного на Тихому океані, коли він ремонтував двигуни бомбардувальників B-24, – він відчував, на що здатне числення. Уявіть собі контрольовану механічно батарею зенітних гармат, що автоматично стріляють по бойовому літаку, що наближається. Числення, припускав він, можна використати, щоб віддавати команду гарматам, у що цілитися.
Щороку близько мільйона американських студентів беруться за вивчення числення. Але значно менше насправді розуміють, про що цей предмет, або можуть сказати, навіщо вивчають його. Це не їх провина. Існує так багато технологій, які потрібно опанувати, так багато ідей, які слід сприйняти, що легко не помітити картини загалом.
Числення – це математика змін. Воно описує все: від поширення епідемії до зиґзаґів добре кинутого бейсбольного м’яча. Предмет є ґарґантюанських розмірів – і такими є його підручники. Обсяг багатьох перевищує 1000 сторінок, і вони чудово служать підпорками для дверей.
Але в межах цієї великої маси ви виявите дві ідеї, які просвічують наскрізь. Усе решта, як казав про "Золоте правило" рабин Гіллел, просто коментарі. Ці дві ідеї – "похідні" й "інтеграли". Кожна домінує на своїй власній половині предмету, названій на її честь, –це диференціальне й інтегральне числення. Загалом, похідна каже вам, як швидко щось змінюється; інтеграл каже вам, скільки його акумульовано. Вони народжені в різні часи, в різних місцях: інтеграли – в Греції близько 250 років до нашої ери; похідні – в Англії та Німеччині в середині XVII ст. Утім, в сюжетній інтризі, просто з новели Діккенса, вони виявилися кровними родичами – хоча щоб побачити сімейну схожість, знадобилося майже два тисячоліття.
У колонці на наступному тижні ми поговоримо про цей неймовірний зв’язок, як і про значення інтегралів. Але спочатку, закладаючи основу, погляньмо на похідні.
Похідні навколо нас, навіть якщо ми не розпізнаємо їх як такі. Наприклад, нахил сходів є похідною. Як усі похідні, він вимірює швидкість змін – тут як далеко ви зайдете вверх чи вниз із кожним вашим кроком. Стрімкі сходи мають велику похідну. Сходи, які пристосовані для інвалідного візка, з невеликим нахилом, мають малу похідну.
Кожна ділянка науки має свої похідні. Вимірюється вона "маржею прибутку", чи "темпами зростання", чи "швидкістю", чи "нахилом", будь-як названа похідна має той самий приємний запах. На жаль, здається, багато студентів після курсу числення виходять із набагато вужчою інтерпретацією, розглядаючи похідну як синонім нахилу кривої.
Їхнє сум’яття зрозуміле. Воно спричинене тим, що ми покладаємося на графіки, щоб виразити кількісні відносини. Укладаючи точки на осі y проти x для візуалізації того, як одна змінна впливає на іншу, всі науковці переводять свої проблеми у спільну мову математики. Швидкість змін, що насправді цікавить їх – швидкість поширення вірусу, швидкість літака чи що-небудь інше – тоді конвертується у щось набагато абстрактніше, але легше для зображення: нахил на графіку.
Як нахили, похідні можуть бути позитивними, негативними чи нульовими, вказуючи на те, що щось зростає, падає чи вирівнюється. Поспостерігайте за грою Майкл Джордана, коли він робить свої найкращі 10 кидків.
Якраз одразу після відривання від землі його вертикальна швидкість (швидкість, з якою його підйом змінюється з часом, а таким чином інша похідна) є позитивною, тому що він рухається вверх. Його підйом збільшується. На шляху вниз ця похідна негативна. І в найвищій точці його стрибка, де він, здається, зависає в повітрі, його підйом якоїсь миті не змінюється і його похідна – це нуль. У цьому сенсі він справді висить.
Тут спрацьовує більш загальний принцип – речі завжди змінюються повільніше на вершині і на дні. Це особливо помітно тут, в Ітаці (штат Нью-Йорк). Найтемніші дні зими не просто немилосердно короткі, вони ледве відрізняються один від одного. Тоді як зараз, коли раптом починається весна, дні швидко стають довшими. Усе це має сенс. Зміна найповільніша на екстремумах саме тому, що похідна тут нуль. Якоїсь миті речі залишаються нерухомими.
Ця нульова похідна, властивість піків і улоговин, лежить в основі найбільш практичних застосувань обчислення. Це дає нам змогу вирахувати, де функція досягне максимуму і мінімуму, питання, яке виникає щоразу, коли ви шукаєте найдешевший і найшвидший спосіб щось зробити.
Мій шкільний учитель містер Джофрей, який начав мене числення, мав дар оживляти ці "максимум-мінімум" питання. Одного дня він ввалився в клас і почав розказувати нам про його прогулянку засніженим полем. Очевидно, вітер надув багато снігу на частину поля, вкривши його товстим шаром і змусивши вчителя пройти цю ділянку набагато повільніше, тоді як решта поля була не засніжена, дозволивши йому легко здолати її. У ситуації, подібній до цієї, він зацікавився, який маршрут повинен вибрати подорожній, щоб якнайшвидше дістатися з пункту A в пункт B.
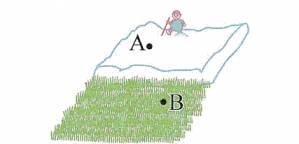
Хтось запропонував пробрести напростець через глибокий сніг, щоб скоротити найповільнішу ділянку шляху. Хоча недоліком цього є те, що решта подорожі займе більше часу, ніж в іншому разі.
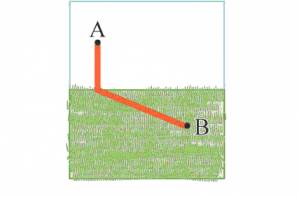
Інша стратегія – прямувати просто від A до B. Це, звичайно, найкоротша відстань, але вона займе додатковий час на найважчій частині подорожі.
Користуючись диференціальним численням, ви можете знайти найкращий шлях. Це, звичайно, особливий компроміс між двома маршрутами, які розглянули вище.
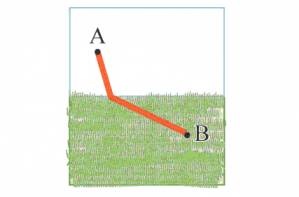
Аналіз включає 4 головні кроки.
Перше, зауважте, що загальний час подорожі – те, що ми саме й намагаємося мінімізувати – залежить якраз від одного числа, відстані x, де подорожній вийде зі снігу.
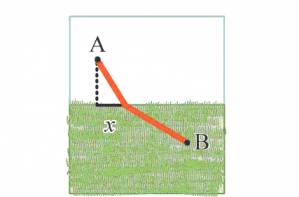
Друге, маючи вибір x і знаючи місцезнаходження точки A і кінцевого пункту B, ми можемо підрахувати, скільки часу подорожній витратить на проходження швидкої та повільної ділянки поля. Для кожного етапу подорожі це обчислення вимагає теореми Піфагора і старої мантри алгебри: "Відстань дорівнює швидкості, помноженій на час". Додавши час обох етапів, ми отримаємо формулу для загального часу подорожі T як функцію x.
Третє, ми зобразимо відношення T до x. Дно кривої – це точка, яку ми шукаємо, вона відповідає найменшому часу подорожі, а отже – найшвидшому маршруту.
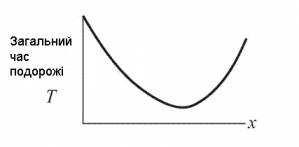
Четверте, щоб знайти найнижчу точку, ми застосуємо принцип нульової похідної, згаданий вище. Ми обчислимо похідну T, яка дорівнює нулю, і знайдемо x.
Ці чотири кроки вимагають знання геометрії, алгебри і різних формул похідної з обчислення – це вміння еквівалентне вільному володінню іноземними мовами і, таким чином, є каменем спотикання для багатьох студентів.
Але кінцева відповідь вартує цих зусиль. Вона відкриває для нас те, що найшвидший шлях дотримується зв’язку, відомого як закон Снелліуса. Що лякає, то це те, що природа також дотримується його.
Закон Снелліуса-Декарта описує, як заломлюються промені світла, коли вони проходять через повітря у воду, і як вони поводяться, сяючи в плавальному басейні. У воді світло рухається повільніше, як подорожній у снігу, і заломлюється так, щоб мінімізувати свій шлях. Схоже світло також заломлюється, коли проходить через повітря в скло чи пластик, як це відображається через лінзи ваших окулярів.
Моторошність ідеї в тому, що світло поводиться так, ніби воно розглядає всі можливі шляхи й автоматично вибирає найкращий. Природа – музична тема в телесеріалі "Зона сутінків" [The Twilight Zone] – якимсь чином знає числення.
Автор: Стівен Строґатц [Steven Strogatz]
Назва оригіналу: Change We Can Believe In
Джерело: The New York Times, 11.04.2010
Зреферував: Михайло Мишкало, Західна аналітична група
| Він нарізає, він ділить на кубики | |
| The New York Times | 23.04.10 |
Часто математичні знаки і символи є загадковими, але більшість із них дають візуальну підказку до власних справжніх значень. Символи нуля, одиниці та безкінечності вдало нагадують порожню діру, одну позначку і безкінечну петлю: 0, 1, ∞. І знак рівності "=" сформовано з двох паралельних ліній, тому що, як сказав 1557 року творець, валлійський математик Роберт Рекорде [Robert Recorde], "жодна з двох речей не може бути більш рівною". У численні найбільш упізнаваним символом є знак інтеграла:
Його граціозні лінії викликають в пам’яті образ музичного ключа або скрипковий f-подібний отвір – чудовий збіг, якщо взяти до уваги, що деякі з найбільш захопливих гармоній у математиці виражені інтегралами. Але справжня причина, чому Ляйбніц вибрав цей символ, є менш поетичною. Це просто видовжений знак S, для "підсумовування". Щодо того, що підсумовують, це залежить від контексту. В астрономії гравітаційне тяжіння Сонця стосовно Землі описано інтегралом. Він становить колективне зусилля всіх мікроскопічних сил, генерованих кожним сонячним атомом на їхніх розмаїтих відстанях від Землі. В онкології зростання маси твердої пухлини можна змоделювати інтегралом. Так само можна змоделювати кумулятивний обсяг ліків, прописаних під час курсу сеансів хіміотерапії. Історично спершу інтеграли виникли в геометрії через проблеми з визначенням площі викривлених форм. Як ми побачили два тижні тому, площу кола можна розглядати як суму багатьох тонких шматків пирога. У межах безкінечно багатьох шматків, кожен з яких є безкінечно тонким, їх можна буде спритно наново укласти у прямокутник, чию площу обчислити набагато легше. Це було типовим використанням інтегралів. Усе, про що в них йде мова, – це саме про те, як узяти щось складне і покроїти та поділити так, щоб було легко все це додати. У тривимірному узагальненні цього методу Архімед (а перед ним Евдокс Кнідський, близько 400 років до нової ери) обчислив об’єми сфер, конусів, бочок, призм й інших розмаїтих твердих форм, подавши їх як штабель багатьох пластинок або дисків, як тонко порізану салямі. Підрахувавши об’єм різних шматків, а тоді майстерно інтегрувавши їх – додавши знову разом – вони змогли обчислити об’єм оригінального цілого предмета. Сьогодні ми все ще просимо математиків і вчених, які подають надії, покращити їх уміння інтегрального числення, використовуючи його для вирішення цих класичних геометричних проблем. Вони є одними з найважчих завдань, які ми даємо, і багато студентів ненавидять їх, але немає надійнішого способу, щоб відшліфувати легкість володіння інтегралами, що необхідне для передової праці в будь-якій дисципліні, пов’язаній з числами, від фізики до фінансів. Одна з таких головоломок стосується об’єму тривимірної ділянки, спільної для двох ідентичних циліндрів, які перетинаються перпендикулярно, як труби від плити на кухні. Щоб зробити чітку візуалізацію цієї форми, потрібно мати неабияку уяву. Отже, немає нічого ганебного в тому, щоб визнати поразку і шукати спосіб, як зробити цю форму більш уявною. Щоб зробити так, ви можете вдатися до трюку, який використовував мій шкільний учитель математики – візьміть бляшанку і зріжте верх ножицями, щоб сформувати циліндричний інструмент для вирізання серцевини. Тоді виріжте серцевину у великій картоплині з Айдахо або шматок пінопласту з двох взаємно перпендикулярних напрямів. Огляньте, не поспішаючи, форму, яку ви отримали в підсумку. Не маючи ні картоплини, ні пінопласту, ми повинні погодитися вирішити це намаганням передати на плоскій поверхні, як виглядає це дивне тіло:
Дивовижно, навіть хоча вона створена з двох круглих циліндрів, вона має квадратні поперечні розтини. Це штабель з безкінечно багатьох шарів, кожен з яких є квадратом, конусоподібний від великого квадрату в середині і спадаючий поступово до менших квадратів, і нарешті до одних точок на верху і на дні. Тепер комп’ютерна анімація робить можливим розкрити структуру форми набагато легше і наочніше.
Усе ж зобразити форму – це просто перший крок. Залишається визначити її об’єм. Архімед зміг обчислити її, але тільки завдяки своїй неймовірній винахідливості. Він використав механічний метод, який базувався на важелях і центрах гравітації, фактично подумки, зважуючи форму, порівнюючи її з іншими, які він уже розумів. Вадою його підходу, крім потреби в надто високих здібностях, було те, що він застосовний тільки до обмеженого ряду форм. Ці концептуальні дорожні блоки ставили в безвихідь найкращих математиків світу протягом наступних 19 століть… аж до середини 1600-х, коли Грегорі, Барроу, Ньютон і Ляйбніц установили те, що сьогодні відомо як фундаментальна теорема числення, або формула Ньютона-Ляйбніца. Фундаментальна теорема є потужним зв’язком між інтегралами і темою попередньої колонки – похідними. Вона значно розширює всесвіт інтегралів, які можна розв’язати, і зводить їх числення до важкої механічної роботи. У наші дні комп’ютери можна запрограмувати на її використання – і так само можуть робити студенти. З її допомогою навіть проблема двох перпендикулярних труб, що свого часу була викликом світового класу, тепер стає вправою в межах, доступних для вирішення звичайному студентові. Непрактично описувати тут саму формулу. Натомість я спробую пояснити, чому вона є таким неймовірним проривом. Вона дозволила математикам значно точніше передбачити змінюваність світу, ніж це коли-небудь було можливо. Найпростіший вид змін можна було обчислити за допомогою алгебри. Коли щось змінюється постійно, з постійною швидкістю, алгебра працює чудово. Це сфера формули "відстань дорівнює швидкості, помноженій на час". Наприклад, автомобіль, який рухається з незмінною швидкістю 60 миль за годину, проїде 60 миль за першу годину і 120 миль на кінець другої години. А як щодо змін, які відбуваються зі змінною швидкістю? Така змінна швидкість всюди навколо нас – у зростанні швидкості пенні, кинутого з високого будинку, у потоках відпливів і припливів, в еліптичній орбіті планет, у наших внутрішніх добових ритмах. І числення може справитися з кумулятивними ефектами змін, настільки неоднакових, як ці. Майже протягом двох тисячоліть після Архімеда існував тільки один метод передбачити чистий ефект змінних змін: додавати різні пласти один за одним. У більшості випадків це неможливо зробити. Було надто важко обчислити безкінечні суми. Формула Ньютона-Ляйбніца дала змогу вирішити багато із цих проблем – не всі, але значно більше, ніж перед тим. Вона часто давала коротший шлях для розв’язання інтегралів, принаймні для елементарних функцій (сум і продуктів степенів, експоненціальних функцій, логарифмів і тригонометричних функцій), що описують так багато явищ у світі природи. Із цієї перспективи спадком інтегрального числення є погляд на всесвіт у стилі кухонного комбайна Veg-O-Matic, який нарізає овочі плястерками. Ньютон і його наступники вчили нас, що природа розкривається шарами. Виявилося, що фактично всі класичні закони фізики, відкриті за останні 300 років, мають цей характер: описують вони рух частинок чи потік тепла, електрики, рух повітря чи води. Разом із законами регулювання, умови на кожному відтинку часу чи простору визначають, що трапиться на наступних відтинках. Наслідки були глибокими і суттєвими. Уперше в історії стало можливим раціональне передбачення… не тільки одного пласта якоїсь миті, але з допомогою формули Ньютона-Ляйбніца – за допомогою стрибків і відскоків. Отже, нам давно потрібно поновити наше гасло для позначення інтегралів з "Вони нарізають, вони ділять на кубики" на "Перерахунок. Кращий маршрут доступний". Автор: Стівен Строґатц [Steven Strogatz] | |
| Мислити теорією груп | |
| The New York Times | 05.05.10 |
Я і моя дружина маємо різні стилі спання – і наші матраци демонструють це. Вона всю ніч збирає свої подушки, перебирає і товче їх, та заледве залишає вм’ятину в матраці, тоді як я лежу на спині, немов мумія, формуючи зі свого боку ліжка вм’ятину у вигляді печери. Виробники матраців рекомендують періодично перевертати матраци, можливо, пам’ятаючи про людей, подібних до мене. Але яка система найкраща? Як насправді ви мали б повернути матрац, щоб у результаті отримати найбільш рівномірне його зношення? Браян Гейс [Brian Hayes] досліджує цю проблему у своїй останній книжці "Теорія груп у спальні" [Group Theory in the Bedroom] – в однойменному есеї. Якщо відкинути двозначні ситуації, "група", про яку тут йдеться, – це сукупність математичних дій: усі можливі способи того, як ви можете перекинути, повернути чи перевернути матрац, щоб він усе ще акуратно лежав на рамі ліжка. Докладно розглядаючи математику матраца, я сподіваюся більш загально передати вам відчуття теорії груп. Це одна з найбільш різносторонніх частин математики. Вона лежить в основі всього: від хореографії контра-денсингу (стиль танцю, коли пари стоять одна напроти одної) і фундаментальних законів фізики елементарних частинок до мозаїк Альгамбри і їх хаотичних двійників, як оце зображення. Як свідчать ці приклади, теорія груп перекидає мости між наукою і мистецтвом. Вона звертається до чогось, що є спільним для двох культур – до постійного захоплення симетрією. Однак оскільки теорія груп містить такий широкий ряд феноменів, то обов’язково є абстрактною. Вона зводить симетрію до її суті. Зазвичай ми думаємо про симетрію як про властивість форми. Але теорії груп зосереджуються більше на тому, що ви можете зробити з формою – надто на всіх способах, за допомогою яких ви можете змінити її, при цьому залишаючи незмінним щось, що властиво їй. Якщо точніше, вони шукають усі трансформації, які залишають форму незмінною, взявши до уваги певні обмеження. Ці трансформації називають "симетріями" форми. Разом вони формують "групу", сукупність трансформацій, зв’язки між якими визначають найбільш базову архітектуру форми. Якщо йдеться про матрац, то трансформації змінюють його положення в просторі (це те, що змінюється), водночас підтримують його негнучкість (це обмеження). І після того, як розвіється дим, матрац повинен акуратно лягти в прямокутну раму ліжка (це те, що залишається незмінним). Подивімося із цими правилами, які трансформації кваліфікують як членство в цій маленькій ексклюзивній групі. Виявляється, тільки чотири з них. Перша трансформація "нічого не робити", лінивий, але популярний вибір, який залишає матраци недоторканими. Вона, звичайно, відповідає всім правилам, але це не надто допомагає продовжити життя вашого матраца. Усе ж дуже важливо включити її в групу. Для теорії груп вона відіграє ту саму роль, що й нуль для додавання чисел або 1 для множення. Математики називають її "елементом ідентичності", отже, я позначив її символом I. Наступними будуть три справжні способи перекидання матраца. Щоб розрізняти їх, корисно буде позначити цифрами кути матраца: Перший спосіб перекидання зображено на початку цього тексту. Симпатичний джентльмен у смугастій піжамі намагається перекинути матрац, повертаючи його на 180 градусів навколо довгої осі рухом, який я назву H – "горизонтальне перекидання". Більш відважний і нерозсудливий спосіб перекинути матрац – це "вертикальний поворот" V. Цей маневр міняє місцями голову і ноги матраца. Ви повинні поставити матрац вертикально, довгим кінцем так, що він майже сягне стелі, а тоді штовхнути його кінець через голову. Чистий ефект, крім надзвичайного глухого удару, полягає в тому, щоб повернути матрац на 180 градусів навколо осі, як це показано внизу. Остання можливість – це крутонути матрац на 180 градусів, при цьому не піднімаючи його з ліжка. На відміну від поворотів H і V, це "обертання" R тримає нагорі верхню поверхню. Це стане очевидно, якщо ми поглянемо на матрац зверху – тепер уявіть, що він є прозорим, і простежте за числами в куті кожної з можливих трансформацій. Горизонтальне перевертання повертає числа у їх дзеркальні відображення. Він також переставляє їх так, що 1 і 2 міняються місцями, як 3 і 4. Вертикальне перевертання переставляє числа по-іншому і ставить їх з ніг на голову, крім їх дзеркальних зоображень. Проте обертання не генерує жодних дзеркальних образів. Воно просто повертає числа догори ногами, цього разу змінюючи 1 на 4 і 2 на 3. Ці деталі не є головною ідеєю. Важливо те, як трансформації пов’язані одна з одною. Зразки їх взаємодії кодують симетрію матраца. Зображення наступної діаграми допоможе нам показати ці зразки із мінімальною затратою зусиль. (У новій чудовій книжці "Візуальна теорія груп" [Visual Group Theory] Натана Картера [Nathan Carter] досить образів, як оцей. Це один з найкращих вступів до теорії груп – або до будь-якого розділу вищої математики, який я коли-небудь читав). У кутах діаграми показано чотири можливі "стани" матраца. Верхній ліворуч є стартовим пунктом. Кольорові стрілки показують рух матраца з одного стану в інший. Наприклад, зелена стрілка, яка показує рух з верхнього лівого до нижнього правого кута, відображає дію обертання R. Також та сама зелена лінія має стрілку з іншого боку, бо якщо ви двічі зробите R, то це рівнозначно "нічого не робити". Це не повинно дивувати. Це просто означає, що перекинути матрац з ніг на голову, а потім ще раз – те саме, що повернути матрац до його початкового стану. Ми можемо належно підсумувати це рівнянням RR = I, де RR означає двічі робити R, а I – це "нічого не робити", елемент ідентичності. Тому горизонтальне і вертикальне перевертання-трансформації також анулюють самі себе: HH = I і VV = I. Діаграма містить багато іншої інформації. Наприклад, вона показує, що зухвалий вертикальний поворот V еквівалентний HR, горизонтальному повороту, за яким слідує обертання – набагато безпечніший шлях для досягнення того самого результату. Щоб перевірити це, почніть зі стартового стану у верхньому лівому куті. Голова матраца слідує на схід вздовж H до наступного стану, а звідти діагонально рухається на південний захід уздовж R. Оскільки ви доходите до того самого стану, який отримали б, якби просто виконали спочатку V, діаграма демонструє, що HR = V. Зауважте також, що порядок виконання цих дій не має значення: HR = RH, оскільки обидва способи приводять до V. Ця байдужість до порядку актуальна для будь-якої пари дій. Ви повинні думати про це як про узагальнення комутативного закону додавання простих чисел, x і y, згідно з яким x + y = y + x. Але будьте уважні: матрацна група є особливою. Багато інших груп порушують комутативний "закон". Ті, кому пощастило дотримуватися його, є особливо чистими і простими. І тепер до результату. Діаграма показує, як отримати спосіб найбільш рівномірного зношення матраца. Будь-яка стратегія, яка періодично застосовує всі чотири стани, спрацьовуватиме. Наприклад, чергування R і H зручне, оскільки воно, оминаючи V, не вимагає значних зусиль. Щоб допомогти вам запам’ятати це, деякі виробники пропонують мнемоніку "крутіння навесні і переворот восени" ["spin in the spring, flip in the fall"]. Матрацна група з’являється в деяких зовсім неочікуваних місцях, від симетрії молекул води до логіки пари електричних перемикачів. Це одна з чарівних рис теорії груп. Вона показує єдність речей, які в іншому разі здавалися б непов’язаними між собою… Немов анекдот про те, як фізик Ричард Фейнман [Richard Feynman] отримав відстрочку від призову в армію. Військовий психіатр попросив Фейнмана виставити руки так, щоб він міг оглянути їх. Фейнман витягнув їх, одна долоня вверх, інша вниз. "Ні, по-іншому", – сказав психіатр. Тож Фейнман повернув обидві руки, залишивши одну долоню донизу, іншу догори. Фейнман не просто грав у розумову забаву; він насолоджувався гумором теорії груп. Якщо ми розглянемо всі можливі способи того, як він міг виставити свої руки, плюс розмаїті переходи між ними, стрілки сформують той самий зразок, що й у матрацній групі! Але якщо все це робить справу з матрацами надто складною, можливо, справжній уроком є той, який ви вже знаєте: якщо щось не дає спокою, просто подумайте про це перед сном. Автор: Стіве Строґатц [Steven Strogatz] | |
Рекомендувати цей матеріал













